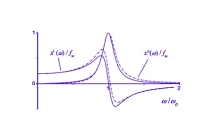
Fractional Calculus

This was the subject of my Ph.D. thesis. My scientific adviser, Professor Ravil' Rashidovich Nigmatullin, exposed me to the idea to use "fractional derivatives" (more rigorously integro-differential operators of Fractional Calculus) in differential equations describing physical phenomena instead of dissipative terms.

The famous example of "fractional oscillator", where time derivative of order less than 2 mimics Lorentian line shape, is shown on the right.

Fractional Oscillator is one of several classic examples which illustrate applications of fractional calculus to physical problems. There are many works which discuss this example. We, together with Professor Alex Puzenko, also published a paper on this subject. I believe that the most interesting result of our work is the operator perturbation series with respect to the order of a fractional derivation which could be used to treat other problems. Especially those, that unlike Fractional Oscillator problem, cannot be solved in closed forms.

Old love never fades. I am still working on these problems, when I can save some time from my main activity.

Related articles:

Y. Ryabov "Behavior of fractional diffusion at the origin", Phys. Rev. E 68: 030102(R) (2003)

Y. Ryabov, A. Puzenko "Damped oscillations in view of the fractional oscillator equation", Phys. Rev. B 66: 184201 (2002)

R.R. Nigmatullin, Y. Ryabov, "Cole-Davidson dielectric relaxation as a self-similar relaxation process", Phys. Solid State 39: 87-90 (1997). By the way, just for the case if anybody interested, I have Russian original of this paper too.